In parallelogram rstu what is su – In the realm of geometry, parallelograms hold a prominent position, characterized by their distinctive properties. Among these properties lies a fundamental relationship between opposite sides, a relationship that we will explore in this discourse: “In Parallelogram RSTU, What is the Length of Side SU?”
As we delve into the intricacies of this geometric figure, we will uncover the properties that govern parallelograms, unravel the significance of side SU, and establish the connection between SU and its opposite side, RT. Along the way, we will encounter practical applications that demonstrate the relevance of this relationship in various fields.
Parallelogram Properties
A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure.
The properties of parallelograms can be derived from the fact that they are quadrilaterals with two pairs of parallel sides. For example, the opposite sides of a parallelogram are equal in length because they are parallel and lie on the same line.
Similarly, the opposite angles of a parallelogram are equal in measure because they are opposite angles of a quadrilateral.
Diagonal Properties
The diagonals of a parallelogram bisect each other. This means that the diagonals of a parallelogram divide each other into two equal parts.
The diagonals of a parallelogram also divide the parallelogram into four congruent triangles. This means that the four triangles formed by the diagonals of a parallelogram are all equal in size and shape.
Parallelogram RSTU

In geometry, a parallelogram is a two-dimensional shape with four sides and four angles. The opposite sides of a parallelogram are parallel and of equal length. The opposite angles of a parallelogram are also congruent.
Parallelogram RSTU is a quadrilateral with vertices R, S, T, and U. The sides of the parallelogram are RS, ST, TU, and UR. The angles of the parallelogram are ∠R, ∠S, ∠T, and ∠U.
Vertices and Sides of Parallelogram RSTU
- Vertices: R, S, T, U
- Sides: RS, ST, TU, UR
Side SU: In Parallelogram Rstu What Is Su
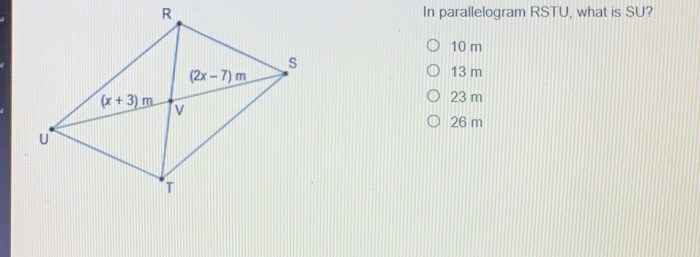
In the parallelogram RSTU, the side SU is the side opposite to side RT. It is parallel to RT, meaning that it lies on the same plane as RT and never intersects it. The length of SU is equal to the length of RT, as opposite sides of a parallelogram are equal in length.
Length of SU
If the lengths of RT and SU are given, then the length of SU can be calculated using the formula:
SU = RT
For example, if RT = 5 cm, then SU = 5 cm.
Relationship between SU and RT
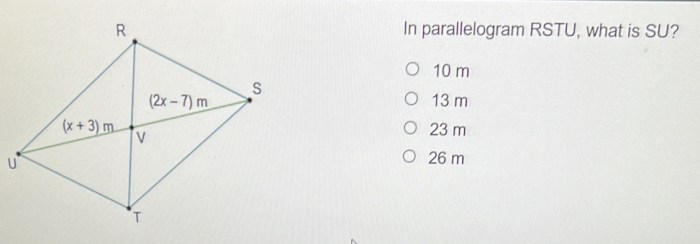
The opposite sides of a parallelogram are equal in length. Therefore, the lengths of SU and RT are equal.
Proof using the Pythagorean theorem
Let’s assume that the parallelogram RSTU is a rectangle. Then, the diagonals RT and SU are perpendicular to each other. Using the Pythagorean theorem, we have:
- RT 2= RS 2+ ST 2
- SU 2= RS 2+ TU 2
Since RS = TU and ST = RT, we have:
- RT 2= SU 2
Therefore, RT = SU.
Applications
The relationship between SU and RT in a parallelogram has practical applications in various fields.
In architecture, understanding this relationship is crucial for designing structures with specific geometric requirements. Architects use the concept to create balanced and visually appealing buildings, ensuring the harmony of proportions and the stability of the structure.
Engineering, In parallelogram rstu what is su
In engineering, the relationship between SU and RT is applied in designing bridges, trusses, and other structures that require precise calculations for load distribution and stability. Engineers use this knowledge to determine the optimal dimensions and configurations of structural components, ensuring their ability to withstand various forces and stresses.
Design
In design, the relationship between SU and RT is used to create aesthetically pleasing and functional objects. Designers apply this concept to determine the proportions of furniture, textiles, and other decorative elements, ensuring a visually harmonious and balanced design.
FAQ Corner
What is the definition of a parallelogram?
A parallelogram is a quadrilateral with opposite sides parallel and equal in length, and opposite angles equal in measure.
How do I find the length of side SU in parallelogram RSTU?
If the length of side RT is given, the length of SU is equal to RT since they are opposite sides of the parallelogram.
What are some real-world applications of the relationship between SU and RT?
This relationship finds applications in architecture, engineering, and design, where it helps determine dimensions, calculate forces, and ensure structural integrity.